MinChiang的博客

# B-树、B树、B+树、B*树

# 基本概念

  • 节点的度：结点拥有的子树数目称为结点的度，叶子结点的度为0；
  • 树的度：树内各个节点的度的最大值；
  • 节点的深度：从根节点（0层或者1层）开始，到该节点层数，自上而下；
  • 节点的高度：从其最下面的叶子节点（0层或者1层）开始，到该节点的层数，自下而上；
  • 树的高度和深度：是相等的，就是树所拥有层的数量。

树高度解释1树高度解释2

图 左 右
层数 从第0层开始 从第1层开始
最大层数 4 5
深度 4 5
高度（高度=深度） 4 5
高度（数层数） 5 5

# B-树与B树

  • B-树和B树是同一个概念；
  • 根结点至少有两个子女；
  • 每个中间节点都包含k-1个元素和k个孩子，其中 m/2 <= k <= m；
  • 每一个叶子节点都包含k-1个元素，其中 m/2 <= k <= m；
  • 所有的叶子结点都位于同一层；
  • 每个节点中的元素有序排列；
  • **每个节点（非节点和子节点）都包含关键字（以及其他数据内容）**以及对应的各个子树的指针；
  • B树检索时，由于每个节点都存放数据信息，因此不用搜索到叶子节点，搜索速度很快，但不稳定；
  • B树顺序读取时，需要用到中序遍历。

B树示例图：

B树示例图

B树插入示例图：

B树插入示例图1

B树插入示例图2

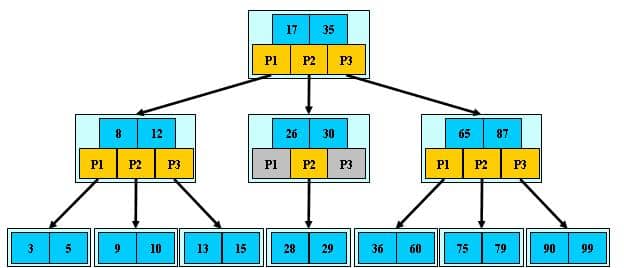
B树删除示例图：

B树删除示例图1

B树删除示例图2

B树删除示例图3

# B+树特征

  • 就是在B树的基础上，在叶子节点加入指针连接；
  • 所有关键字（含数据）都出现在叶子节点中（密集索引）；
  • B+树比B树更加矮胖，因为B+树的非叶子节点仅存储关键字和对应子节点的指针，不存对应额外的数据内容，因此理论上来说，相同容量的空间可以存储更多的索引数据；
  • B+树查询更加稳定，但是查询相比B树会慢；
  • B+树具备排序功能，叶子节点构成有序链表，有利于做顺序扫描。

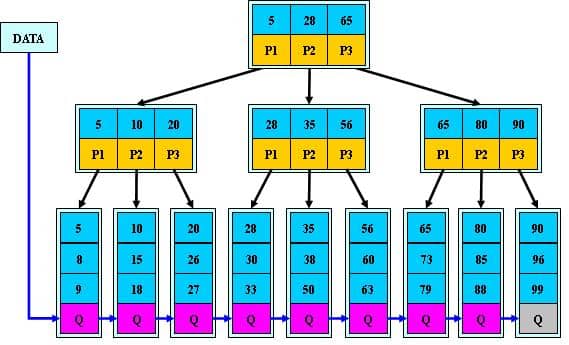
B+树示例图

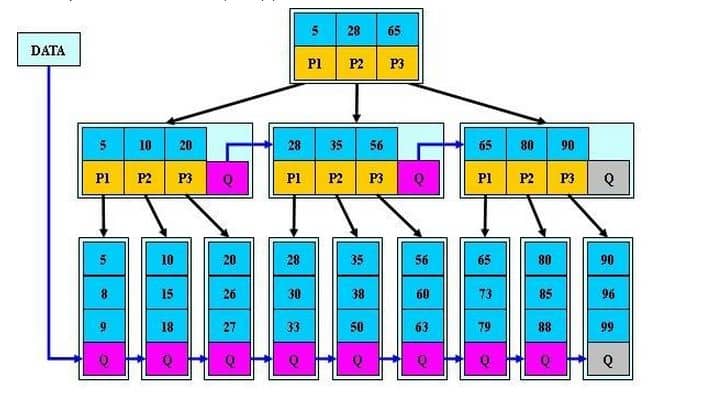
# B*树特征

  • B*树在非叶子节点中加入兄弟节点的指针；
  • B*树初始化关键字数量更多，使节点空间利用率更高；
  • 分裂时，B*树先检查兄弟节点是否满，未满时会向兄弟节点转移。

B星树示例图

# 二叉搜索树

public class BinaryTree {

    TreeNode root;

    public BinaryTree(int[] arr) {
        this.create(arr);
    }

    public void create(int[] arr) {
        if (arr == null || arr.length == 0) {
            return;
        }
        root = new TreeNode(arr[0]);
        for (int i : arr) {
            insert(i);
        }
    }

    public TreeNode search(int e) {
        TreeNode now = root;
        while (now != null) {
            if (now.val == e) {
                return now;
            } else if (now.val > e) {
                now = now.left;
            } else {
                now = now.right;
            }
        }
        return null;
    }

    public TreeNode insert(int e) {
        if (root == null) {
            root = new TreeNode(e);
            return root;
        }

        TreeNode now = root, result = new TreeNode(e);
        while (true) {
            if (e > now.val) {
                if (now.right == null) {
                    now.right = result;
                    return result;
                } else {
                    now = now.right;
                }
            } else if (e < now.val) {
                if (now.left == null) {
                    now.left = result;
                    return result;
                } else {
                    now = now.left;
                }
            } else {
                return now;
            }
        }
    }

    public TreeNode delete(int e) {
        TreeNode now = root, pre = null;
        while (now != null) {
            if (now.val == e) {
                break;
            } else if (now.val > e) {
                pre = now;
                now = now.left;
            } else {
                pre = now;
                now = now.right;
            }
        }

        if (now == null) {
            return null;
        }

        if (now == root) {
            root = null;
            return now;
        }

        boolean leftEmpty = (now.left == null);
        boolean rightEmpty = (now.right == null);
        if (leftEmpty && rightEmpty) {
            pre.left = null;
            pre.right = null;
        } else if (!leftEmpty && !leftEmpty) {
            if (now.val < pre.val) {
                pre.left = now.right;
            } else {
                pre.right = now.right;
            }
            TreeNode min = now.right;
            while (min.left != null) {
                min = min.left;
            }
            min.left = now.left;
            now.left = null;
        } else {
            TreeNode sub = (leftEmpty ? now.right : now.left);
            if (now.val < pre.val) {
                pre.left = sub;
            } else {
                pre.right = sub;
            }
        }
        return now;
    }

    public void preOrder(TreeNode node) {
//        if (node == null) {
//            return;
//        }
//
//        System.out.println(node.val);
//        preOrder(node.left);
//        preOrder(node.right);
        Stack<TreeNode> stack = new Stack<TreeNode>();
        while (node != null || !stack.empty()) {
            if (node != null) {
                System.out.println(node.val);
                stack.push(node);
                node = node.left;
            } else {
                node = stack.pop();
                node = node.right;
            }
        }
    }

    public void midOrder(TreeNode node) {
//        if (node == null) {
//            return;
//        }
//        midOrder(node.left);
//        System.out.println(node.val);
//        midOrder(node.right);
        Stack<TreeNode> stack = new Stack<TreeNode>();
        while (node != null || !stack.empty()) {
            if (node != null) {
                stack.push(node);
                node = node.left;
            } else {
                node = stack.pop();
                System.out.println(node.val);
                node = node.right;
            }
        }
    }

    public void posOrder(TreeNode node) {
//        if (node == null) {
//            return;
//        }
//        posOrder(node.left);
//        posOrder(node.right);
//        System.out.println(node.val);
        Deque<TreeNode> deque = new ArrayDeque<>();
        TreeNode r = null;
        while (node != null || !deque.isEmpty()) {
            if (node != null) {
                deque.push(node);
                node = node.left;
            } else {
                node = deque.peek();
                if (node.right == null || node.right == r) {
                    System.out.println(node.val);
                    r = node;
                    deque.pop();
                    node = null;
                } else {
                    node = node.right;
                }
            }
        }
    }

    public TreeNode getMin() {
        TreeNode now = root;
        while (now.left != null) {
            now = now.left;
        }
        return now;
    }

    public TreeNode getMax() {
        TreeNode now = root;
        while (now.right != null) {
            now = now.right;
        }
        return now;
    }

    public static class TreeNode {

        int val;
        TreeNode left;
        TreeNode right;

        public TreeNode(int val) {
            this.val = val;
        }

        public TreeNode() {
        }

    }

}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211

# 二叉堆

public class HeapSort<T extends Comparable<T>> {

    private T[] arr;

    public HeapSort(T[] arr) {
        this.arr = Arrays.copyOfRange(arr, 0, arr.length);
        adjust();
    }

    /**
     * 初始化调整节点
     */
    private void adjust() {
        //遍历非叶子节点
        int mid = arr.length / 2 - 1;
        int left, right;
        while (mid >= 0) {
            down(mid);
            mid--;
        }
    }

    /**
     * 数据下沉操作
     *
     * @param mid 需要下沉的元素
     */
    private void down(int mid) {
        //判断是否为叶子节点
        if (mid > arr.length / 2 - 1) {
            return;
        }

        int right = (mid + 1) * 2, left = right - 1;
        if (arr.length > right) {
            int point = arr[left].compareTo(arr[right]) < 0 ? left : right;
            if (arr[point].compareTo(arr[mid]) < 0) {
                T tmp = arr[point];
                arr[point] = arr[mid];
                arr[mid] = tmp;
                //下沉操作
                down(point);
            }
        } else {
            if (arr[left].compareTo(arr[mid]) < 0) {
                T tmp = arr[left];
                arr[left] = arr[mid];
                arr[mid] = tmp;
                //下沉操作
                down(left);
            }
        }
    }

    /**
     * 数据上浮操作
     *
     * @param index 需要下沉的元素
     */
    private void up(int index) {
        if (index == 0) {
            return;
        }
        //获取父节点
        int mid = (index + 1) / 2 - 1;
        if (arr[index].compareTo(arr[mid]) < 0) {
            T tmp = arr[index];
            arr[index] = arr[mid];
            arr[mid] = tmp;
            up(mid);
        }
    }

    /**
     * 获取最大元素
     *
     * @return 最大元素
     */
    public T peek() {
        return arr[0];
    }

    /**
     * 获取并删除最大元素
     *
     * @return 最大元素
     */
    public T pop() {
        T result = peek();
        arr[0] = arr[arr.length - 1];
        arr = Arrays.copyOfRange(arr, 0, arr.length - 1);
        down(0);
        return result;
    }

    /**
     * 插入数据
     *
     * @param t 待插入的数据
     */
    public void push(T t) {
        arr = Arrays.copyOf(arr, arr.length + 1);
        arr[arr.length - 1] = t;
        up(arr.length - 1);
    }

    @Override
    public String toString() {
        return "HeapSort{" +
                "arr=" + Arrays.toString(arr) +
                '}';
    }

}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114

← 算法 →